📝【LeetCode】84 柱状图中最大的矩形
这道题是 LeetCode 84 题。
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1。求在该柱状图中,能够勾勒出来的矩形的最大面积。
解法一:暴力(遍历不同的高度)
遍历每个高度,计算该高度下的最大的连续矩形面积。外层循环遍历每个高度,内层循环从头到尾遍历整个数组即可。使用一个 HashMap 记录已经计算过的高度,不重复计算。
这种方法相当于使用一根从下到上、逐渐升高的水平线,截去水平线上方的部分,统计水平线下方的连续矩形面积。
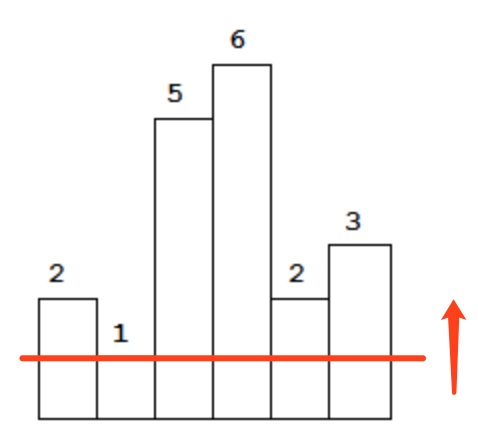
时间复杂度 $O(n^2)$。
空间复杂度 $O(1)$。
代码:
func largestRectangleArea(heights []int) int {
res := 0
set := map[int]bool{}
for _, curHeight := range heights {
if _, ok := set[curHeight]; ok {
continue
}
set[curHeight] = true
preIndex := -1 // 前一个高度小于当前柱高 curHeight 的柱子下标
for i, h := range heights {
if h < curHeight {
// 在此时,i 是下一个高度小于当前柱高的柱子下标
// i-preIndex-1 即高度大于等于当前柱高的连续柱子个数
res = max(res, curHeight*(i-preIndex-1))
preIndex = i
}
i++
}
res = max(res, curHeight*(len(heights)-1-preIndex))
}
return res
}
解法二:分治
此解法来自 LeetCode 题解。
根据木桶原理,一只木桶盛水的多少取决于桶壁上最短的那块。因此,如果选择某个区间内的全部柱子构成一个矩形,那么这个矩形的最大面积取决于区间内最矮的柱子,其面积等于 区间宽度×最矮的柱子高度。
对于这道题,可以先找到整个区间的最矮的柱子,计算上述矩形面积,然后递归地计算最矮柱子左右区间的矩形面积。
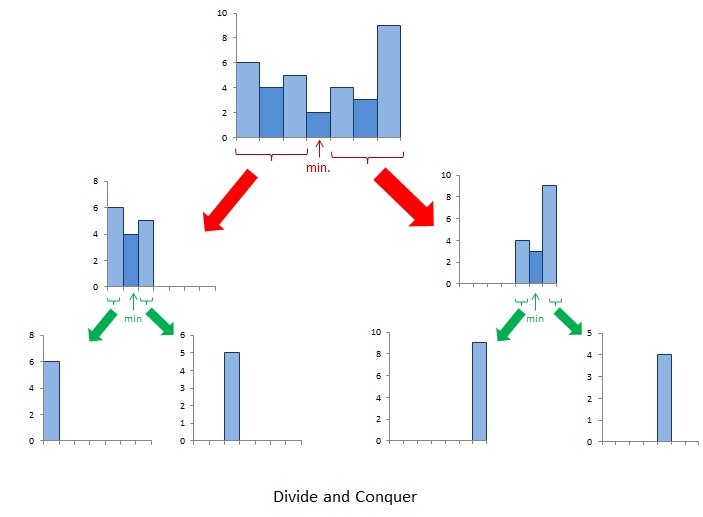
图片来自:LeetCode 题解
时间复杂度:平均 $O(nlogn)$,但是如果数组中的数字是有序的,将退化为 $O(n^2)$。
代码:
func largestRectangleArea(heights []int) int {
if len(heights) == 0 {
return 0
}
return dfs(heights, 0, len(heights)-1)
}
func dfs(heights []int, start, end int) int {
if start > end {
return -1
}
if start == end {
return heights[start]
}
minIndex := start
for i := start + 1; i <= end; i++ {
if heights[i] < heights[minIndex] {
minIndex = i
}
}
curMax := (end - start + 1) * heights[minIndex]
leftMax := dfs(heights, start, minIndex-1)
rightMax := dfs(heights, minIndex+1, end)
return max(curMax, max(leftMax, rightMax))
}
解法三:分治+线段树
此解法来自 LeetCode 题解。
这种解法是解法二的优化。在解法二中,我们需要查找某个区间的最小值,平均时间复杂度是 $O(nlogn)$,但是如果数组中的数字是有序的,将退化为 $O(n^2)$。
对于区间最值的查询问题,可以使用线段树来优化。引入线段树后,无论区间整体是否有序,都可以在 $O(logn)$ 的时间里找到某段区间的最小值。关于线段树的实现,可以查看我之前的文章,此处不再赘述。
相比于解法二,只需修改一处代码:查找区间最小值下标,从遍历查找改为线段树查找。
时间复杂度:$O(nlogn)$。
空间复杂度:$O(n)$,是线段树的空间开销。
代码:
func largestRectangleArea(heights []int) int {
if len(heights) == 0 {
return 0
}
root := BuildSegmentTree(heights, 0, len(heights)-1) // 1. 构建线段树
return dfs(root, heights, 0, len(heights)-1)
}
func dfs(sTree *SegmentTreeNode, heights []int, start, end int) int {
if start > end {
return -1
}
if start == end {
return heights[start]
}
minIndex := sTree.Query(heights, start, end) // 2. 使用 Query() 方法查找区间最小值的下标
curMax := (end - start + 1) * heights[minIndex]
leftMax := dfs(sTree, heights, start, minIndex-1)
rightMax := dfs(sTree, heights, minIndex+1, end)
return max(curMax, max(leftMax, rightMax))
}
线段树代码:
type SegmentTreeNode struct {
start int
end int
min int // 本题线段树节点保存的不是区间最小值,而是最小值所在的下标
left *SegmentTreeNode
right *SegmentTreeNode
}
func BuildSegmentTree(nums []int, left, right int) *SegmentTreeNode {
if left > right {
return nil
}
root := &SegmentTreeNode{left, right, left, nil, nil} // 根据节点区间的左边界值初始化
if left == right {
return root
}
mid := (left + right) / 2
root.left = BuildSegmentTree(nums, left, mid)
root.right = BuildSegmentTree(nums, mid+1, right)
if nums[root.left.min] < nums[root.right.min] {
root.min = root.left.min
} else {
root.min = root.right.min
}
return root
}
func (root *SegmentTreeNode) Query(nums []int, start, end int) int {
if start > root.end || end < root.start {
return -1
}
if start <= root.start && end >= root.end {
return root.min
}
leftMin := root.left.Query(nums, start, end)
rightMin := root.right.Query(nums, start, end)
if leftMin < 0 {
return rightMin
}
if rightMin < 0 {
return leftMin
}
if nums[leftMin] < nums[rightMin] {
return leftMin
}
return rightMin
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
解法四:暴力(遍历不同的柱子)
首先思考:包含某个柱子 i、并且以 heights[i] 为高的最大矩形面积是多少?
显然,对于每个柱子 i,我们只需要以该柱子为中心,向左找到第一个 left 满足 heights[left] < heights[i],向右找到第一个 right 满足 heights[right] < heights[i],left 与 right 之间就是我们要找的矩形,其面积等于 heights[i] × (right-left-1)。
如下图所示,以柱子 i=4 为高的最大面积的矩形,就是红色方框所围的部分。向左找到 left=1,向右找到 right=6(数组的右边界,高度可以视为 0),满足 heights[left], heights[right] < heights[i]。
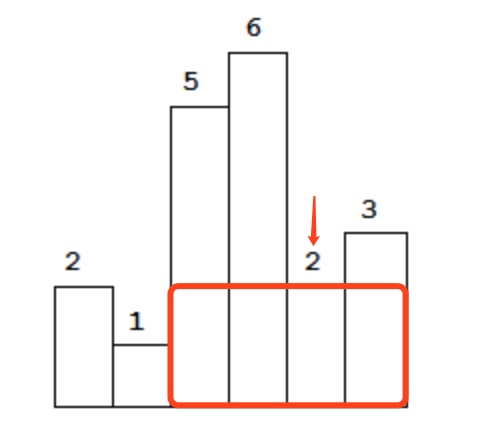
我们可以遍历每个柱子,重复上述过程,输出最大的面积。注意解法四与解法一的区别:解法一是遍历每个高度,解法四是遍历每个柱子。
时间复杂度 $O(n^2)$。
空间复杂度 $O(1)$。
代码:
func largestRectangleArea(heights []int) int {
res := 0
for i, h := range heights {
left, right := i, i
for left > 0 && heights[left-1] >= h {
left--
}
for right < len(heights)-1 && heights[right+1] >= h {
right++
}
res = max(res, h*(right-left+1))
}
return res
}
解法四优化:遍历不同的柱子 + 动态规划
这里采用类似42. 接雨水的解法四的方法,使用两个数组分别记录第 i 个柱子左、右第一个比它矮的柱子下标。时间复杂度可以优化为 O(n)。代码略。
解法五:单调栈
这种解法相当于解法四的优化版。在解法四中,对于每个柱子 i,我们需要以该柱子为中心,向左、向右分别找到第一个比它矮的柱子。一共需要 $O(n^2)$ 的时间复杂度。
引入单调栈可以优化这个过程,一趟遍历就能找到所有柱子的 left、right。单调栈即满足单调性的栈结构,如果当前入栈元素比栈顶元素小,需要将栈顶元素弹出,直到当前入栈元素不小于栈顶元素。
对于这道题,我们使用单调栈保存元素的下标,从左到右遍历所有元素,并维护单调栈。
在解法四的思路的基础上,我们设栈顶元素 stack[top] 就是柱子 i,那么 stack[top-1] 就是柱子 i 左侧第一个比它矮的柱子的下标,记为 left。如果当前遍历的元素 j 的高度小于栈顶元素的高度,那么我们就找到了柱子 i 右侧第一个比它矮的柱子的下标,记为 right。根据 left 和 right,我们可以计算出包含柱子 i 的最大矩形的面积:
heights[i] × (right-left-1) // 其中 i=stack[top], left=stack[top-1], right=j
算法的流程:如果当前遍历元素的高度大于等于栈顶元素的高度,就将当前下标入栈;否则,不断将栈顶元素出栈,同时根据上述公式计算矩形的面积,直到当前遍历的元素的高度不小于栈顶元素的高度,将当前下标入栈。
为了方便,我们先在数组首尾插入 0,表示数组左右边界外侧的高度为 0,然后将下标 0 入栈,从下标 1 开始遍历。这样所有边界情况都可以统一处理。
以 [2, 1, 5, 6, 2, 3] 为例,过程如下:
- 初始化:
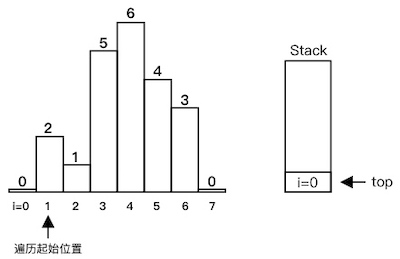
- 开始遍历。
heights[1] > heights[stack[top]=0],入栈:
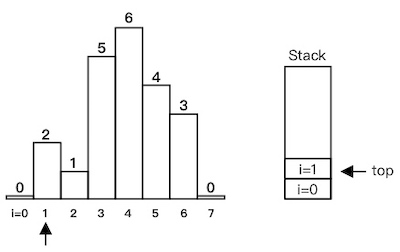
heights[2] < heights[1],出栈,计算红色部分面积,然后i=2入栈。可以看到,红色部分正好位于栈顶下一个元素与当前遍历元素之间,下同:
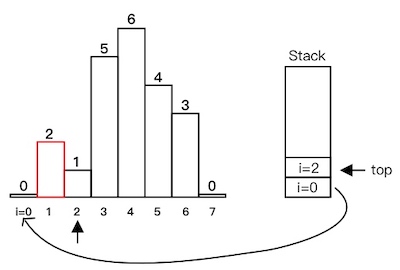
i=3、i=4依次入栈:
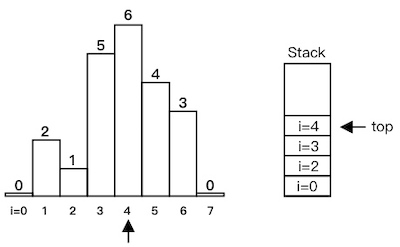
heights[5] < heights[4],出栈,计算红色部分面积:
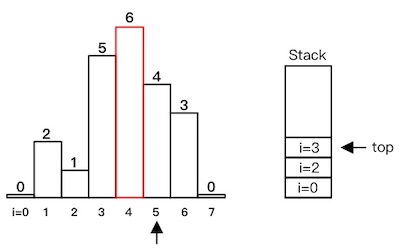
heights[5] < heights[3],出栈,计算红色部分面积,然后i=5入栈:
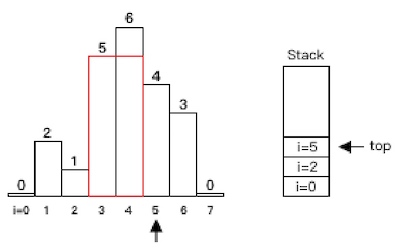
heights[6] < heights[5],出栈,计算红色部分面积:
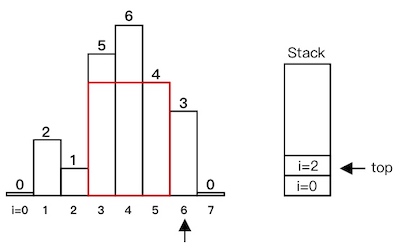
i=6入栈:
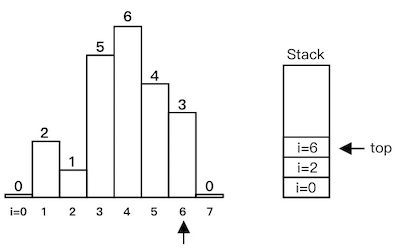
heights[7] < heights[6],出栈,计算红色部分面积:
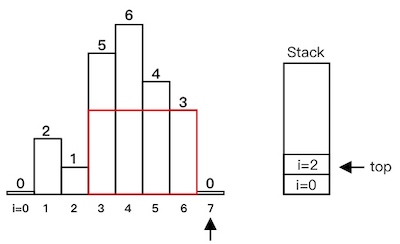
heights[7] < heights[2],出栈,计算红色部分面积:
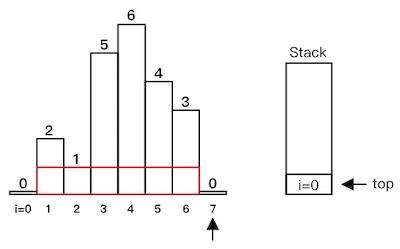
- 遍历结束,输出计算过的最大面积
时间复杂度:$O(n)$,仅需一趟遍历。这种解法打败了 100% 的 golang 提交。
空间复杂度:$O(n)$。
代码:
func largestRectangleArea(heights []int) int {
res := 0
heights = append([]int{0}, heights...)
heights = append(heights, 0) // 首尾添加 0
stack := NewStack()
stack.Push(0) // 下标 0 入栈
for i := 1; i < len(heights); i++ { // 从 1 开始遍历
for heights[i] < heights[stack.Top()] {
h := heights[stack.Pop()]
left, right := stack.Top(), i
res = max(res, h*(right-left-1))
}
stack.Push(i)
}
return res
}
// 以下是栈的模板代码
type ElementType = int
type Stack struct {
s []ElementType
}
func NewStack() *Stack {
return &Stack{
s: make([]ElementType, 0),
}
}
func (s *Stack) Empty() bool {
return len(s.s) == 0
}
func (s *Stack) Top() ElementType {
if s.Empty() {
return 0
}
return s.s[len(s.s)-1]
}
func (s *Stack) Pop() ElementType {
if s.Empty() {
return 0
}
t := s.s[len(s.s)-1]
s.s = s.s[:len(s.s)-1]
return t
}
func (s *Stack) Push(v ElementType) {
s.s = append(s.s, v)
}
总结
本文提供了 3 种思路,5 种解法,从最简单的暴力法开始,不断优化降低时间复杂度。可以看到,即使是相同的思路,采用不同的数据结构,也会有不同的效率。本题涉及分治法、线段树、单调栈的应用,值得回味。
本文发表在我的博客 https://imageslr.com/。我也会分享更多的题解,一起交流,共同进步!
- 版权声明:本文采用知识共享 3.0 许可证 (保持署名-自由转载-非商用-非衍生)
- 发表于 2020-02-02