前言

  • 三种编码方式：无符号、补码、浮点数。分别对应自然数、整数、实数
  • 二进制的整数运算构成一个阿贝尔群，满足整数满足交换律、结合律等，可能溢出
  • 浮点数不一定满足交换律，结合律，因为它只是近似表示

信息存储

存储单位

  • 位（bit）：一个二进制位就是一比特
  • 字节（byte）：8 位构成一个字节。计算机最小的可寻址的内存单位是字节，而不是单独的位
  • 字（word）：2 个字节，即 16 位构成一个字。Intel 是从 16 位体系扩展成 32 位的，因此用术语“字（word）”表示 16 位数据类型，称 32 位数为“双字（double words）”，称 64 位数为“四字（quad words）”
  • 字长（word size）：虚拟地址空间的最大大小，也即“32 位、64 位”机器的含义。字长是指针数据的标称大小（nominal size），如 char * 类型的字节数就是 4（32 位机）或 8（64 位机）

变量大小

程序中声明的变量有不同的大小，如 int 是 4 字节、long 是 8 字节。这些变量在内存中按照 16 位对齐（一个 word）。这样硬件工作更高效。

指针变量的大小等于机器字长。

寻址和字节顺序

多字节对象连续存储，对象的地址是所使用字节的最小地址。如 4 字节的 int 变量，其地址是第一个字节的地址。

如前文所述，计算机最小的可寻址的内存单位是字节，而不是单独的位。换句话说，存储的时候以字节为单位而不是以位为单位。内存地址以字节为单位，0x101 和 0x102 两个内存地址相差了 1 个字节（8 位比特）。

大端法与小端法

按照有效字节在内存中的存储顺序，可以分为大端法和小端法：大端法从高位到低位存储，小端法从低位到高位存储。比如某个 int 型整数的值为 0x01234567，存储在 0x100~0x103 的内存地址上。大端法和小端法的字节顺序如下所示：

-w500

可以看到，将内存从小到大、从左向右书写时，大端法更符合人的阅读顺序。

注意，大端法、小端法存储的基本单位是字节，即一次存储 8 位。

如何判断一台机器是大端法还是小端法？

只需读出某个数字在内存中的第一个字节，即可判断。但是采用 a & 0xff 的方法是行不通的，因为这样读出来的一定是 a 转成数字后的最后一个字节，而不是 a 在内存中实际存储的低位字节。

int main() {
  int number = 1;
  if (*(char *)&number)
    std::cout << "Little-endian!\n";
  else
    std::cout << "Big-endian!\n";
  return 0;
}

如何按内存地址顺序从低到高输出一个变量的全部字节？

假如 a 是一个 int 型变量，则可以将 a 看作长度为 4 的 char 数组。使用 char* 类型的指针可以读取其每一位：

void show_bytes(char* start, size_t len) {
  for (size_t i = 0; i < len; i++) {
    printf("%.2x ", start[i]);
  }
}

void show_int(int x) {
  show_bytes((char*)&x, sizeof(int));
}

int main() {
  show_int(12345);
  return 0;
}

可以看到，取地址运算符 & 创建了一个 int 类型的指针，然后通过强制类型转换，将其转换为 char* 类型的指针，指向一个字节数组。这样就可以依次读取 int 的每个字节。

12345 的十六进制表示为 0x00003039，在不同机器上的输出值如下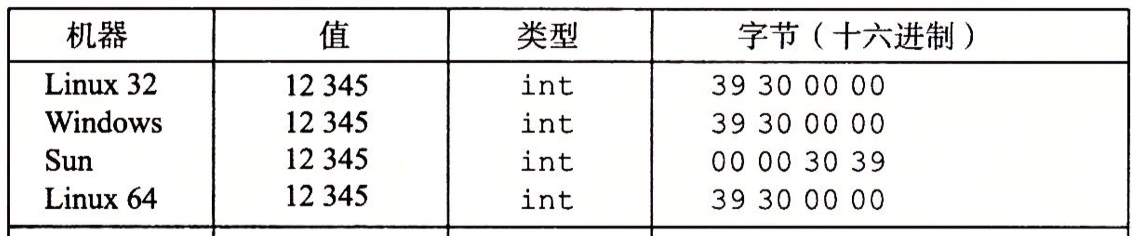： -w572 Linux 上先输出最低有效字节，说明它是小端法机器。

一道面试真题

判断以下程序在 32 位机器上的输出：

int main() {
  int a = 0x1234;
  char *p = (char *)&a;
  printf("%02x\n", *p);
  printf("%02x\n", *(p + 1));
  printf("%02x\n", *(p + 2));
  return 0;
}

根据上文描述，如果机器是大端法，那么变量 a 在内存中地址从低到高依次为：00 00 12 34，共 4 个字节；反之，如果机器是小端法，那么变量 a 在内存中地址从低到高依次为：34 12 00 00。

指针 p 始终指向 a 在内存中的最低位，这是因为取地址运算符返回的也是变量的字节的最小地址。在大端法机器中，p 指向 00；在小端法机器中，p 指向 34。对 char* 指针加 1，相当于令其所指的地址增加一字节。

因此，在小端法机器中，上面的程序输出为：

34
12
00

在大端法机器中，上面程序的输出为：

00
00
12

布尔代数

位级运算

取反 NOT(~)、与 AND(&)、或 OR(|)、异或 EXCLUSIVE-OR(^)。第一个是单目运算，其他都是双目运算。

位运算的应用

位向量形如 1110011010...。可以使用位向量表示集合，与(&)和或( )运算分别表示求并集和求交集。

与(&)实现掩码运算，从一个字中选出某些位。

异或，无需中间变量即可交换两个值：

void inplace_swap(int x, int y) {
  y = x ^ y
  x = x ^ y // 前两步相当于：x = x ^ x ^ y = y
  y = x ^ y // 这一步相当于：y = y ^ x ^ y = x
}

异或还可以找出一堆数组中唯一的、只出现奇数次的数字。

C 语言中的逻辑运算

与、或、非：&&、   、!
注意区分逻辑运算的与或非和位级运算的与或非（&、 、~)，二者完全不同：
  1. 逻辑运算返回值只有 0 或 1
  2. 逻辑运算是短路运算

移位操作

逻辑右移：左端补 0 算术右移：左端补符号位

移动 k 位、k 很大的时候，只会移动 k mod w 位，这里 w 是机器字长。如 32 位机器上，左移 40 位，只会执行左移 8 位。

整数表示

无符号数与有符号数（补码）

无符号数，二进制转为十进制：$B2U_w(X)=\sum^{w-1}_{i=0}{x_i2^i}$，其中 X 是一个数字的二进制表示，$x_i$ 是 X 的第 i 位。

有符号数采用补码表示。有符号数，二进制转为十进制：$B2U_w(X)=-x_{w-1}2^{w-1}+\sum^{w-2}_{i=0}{x_i2^i}$，其中 X 是一个数字的二进制表示，$x_i$ 是 X 的第 i 位。

有符号数的最高有效位就是符号位，其权重为 $-2^{w-1}$。而无符号数中，最高有效位的权重为$2^{w-1}$。

补码的取值范围：

  • 最小值：$TMin_w=-2^{w-1}$，即 1000...00
  • 最大值：$TMax_w=\sum^{w-2}_{i=0}{x_i2^i}$，即 0111...11

补码的范围是不对称的，一半负数个数，一半非负数，TMin 没有相对应的正数。比如 4 位补码的表示范围为 -8~7，对半分为 -8~-1，0~7。

为什么要用补码，而不是原码或者反码

原码最高位充当符号位，0 为正、1 为负。 反码最高位权值为 $-(2^{w-1}-1)$。 补码最高位权值为 $-2^{w-1}$。

原码和反码对于数字 0 都有两种不同的编码方式：原码有 +0 [000…0] 和 -0 [100…0]，反码有 +0 [000…0] 和 -0 [111…1]。

补码的术语来源

对于一个负数 -x，其二进制补码等同于：对于非负数 x，$2^w-x$ 的无符号表示。

有符号数与无符号数的转换

C 语言中，有符号数和无符号数比较时，有符号数会隐式转换为无符号数。

类型转换不会改变位模式，只会改变这些位的解释方式。

扩展与截断

扩展：左侧增加位，如 8 位数字扩展为 16 位数字。 截断：左侧截去位，如 16 位数字截断为 8 位数字。

  • 无符号数的扩展：左侧增加 0
  • 补码数的扩展：左侧增加符号位

二者均能保持值不变。补码数如果是负数，新增加的符号位权值为 $-2^{k}$，而旧的符号位权值由 $-2^{k-1}$ 变为 $2^{k-1}$，抵消了增量。

截断就是丢弃高位。无论是无符号数还是补码数，在位级表示上都是一样的，都是去掉前几位。在位的解释上，一个解释成无符号数，一个解释成有符号数。

二者同时存在

先扩展位、再改变符号。比如从 short 转化为 unsigned 时，先扩展位大小，再有符号数转为无符号数。

整数运算

检测无符号数的加法溢出

两数相加，和小于任一加数。即 s=x+y，若 s<x（等价的，s<y），则溢出。

补码加法的溢出

  • 负溢出：两个负数相加，和比 TMin 还要小，发生负溢，最终结果变为正数
  • 正溢出：两个正数相加，结果比 TMax 还要大，发生正溢，最终结果变为负数

检测补码加法的溢出

  • 两个正数相加，得到负数，发生正溢出。
  • 两个负数相加，得到正数，发生负溢出。

编程实现

以 go 语言为例。最简单的方法是，用 64 位数表示 32 位的边界：

tmin := -1 << 31
tmax := 1<<31-1
if res < tmin || res > tmax {
    // int32 溢出
}

或者根据上面的“同号相加，结果变号”来判断是否发生溢出。

补码的非

一个数的非就是它的相反数（逆元），两数相加为 0。

补码的非：如果 x > TMin，其补码的非为 -x；如果 x == TMin，其补码的非为 x。

设 x = TMin 的补码表示为 [111…1]，则 x + x = TMin + TMin = [111…1] + [111…1] = 1[000…0] = 0，前面溢出的 1 被丢弃了。

补码非的位级表示有两种。第一种是对每一位取反，再对结果加 1，表示为 C 语言式子：-x == ~x+1。

这种思路可以这样理解：对 x 每一位都取补，那么这个数和 x 加起来是 11111111…1；再将结果加 1，就会让其不断进位直到溢出，结果变为 0。因此按位取反再加 1 就是 x 的非。

另一种方法是找到补码位向量的最右边的 1 的位置，然后对其左边的所有位取反（不包括这个 1）。这种方法和第一种的思路其实是一致的。

补码加法、补码乘法

无论是加法还是乘法，无符号数和补码数的运算的位级表示都是一样的。一个将结果解释为无符号数，一个解释为有符号数。

检测乘法溢出

使用除法。见练习题 2.35

乘以常数 -> 移位和加法

当乘以一个常数时，编译器会使用移位和加法运算的组合来代替乘以常数。

比如 x*14，由于 $14=2^3+2^2+2^1$，所以会将乘法重写为 (x<<3)+(x<<2)+(x<<1)；还可以利用 $14=2^4-2^1$，将其改写为 (x<<4)-(x<<1)。

除以 2 的幂 / 模运算

无符号和补码数分别使用逻辑移位和算术移位代替除以 2 的幂。

整数除法需要向 0 舍入。无符号数和补码的移位运算都是向负无穷舍入。无符号数由于数值非负，因此等同于是向 0 舍入。补码数在数组为正时，等同于向 0 舍入；数值为负时，却是向负无穷舍入，导致结果不准确。

解决方法是增加一个 bias。如果被除数是负数，那么需要加上一个偏置来向上舍入。偏置是 2^k-1。

C 语言中，数字都是用补码表示。在除法运算时，编译器会自动地增加这个偏置。C 表达式：

(x<0 ? x+(1<<k)-1 : x) >> k

会计算数值 $x/2^k$。

推广：模运算（编程除法）向上取整

  • 向下取整：a / b
  • 向上取整：a+b-1 / b

原理同上文除以 2^k 时增加 bias 2^k-1 以向上取整。

浮点数

IEEE 浮点表示

公式表示：$V=(-1)^s×M×2^E$

  • 符号位 s(sign)：正数还是负数
  • 尾数 M(significand)：二进制小数
  • 阶码 E(exponent)：对浮点数加权

编码表示：将浮点数的位分为三个字段

  • 符号位 1 位，直接编码符号 s
  • k 位阶码字段 exp 编码阶码 E。注意 exp 不等于 E，E 等于 e-Bias 或者 1-bias，见下文
  • n 位小数字段 frac 编码尾数 M，同样编码出来的值不一定等于 M，依赖于阶码字段的值 exp 是否为 0

根据 exp 的值，被编码的值可以分为 3 种不同情况：

  • 规格化的：阶码不全 0、不全 1
    • 阶码的值被解释以偏置形式表示的有符号整数，阶码字段 exp 表示的指数为 E=e-Bias，其中 e 是 k 位阶码字段表示的无符号数，Bias 等于 $2^{k-1}-1$
    • 小数字段 frac 表示的尾数为 M=1+f，f 为小数字段表示的小数值，尾数隐含的以 1 开头
  • 非规格化的：阶码全 0
    • 解码值是 E=1-Bias。不设置为 -Bias 是为了获得平滑的过渡
    • 尾数 M=f，不包含隐含的 1
    • 数值 0 可以表示为除符号位以外全是 0，这样有正 0 和负 0
  • 特殊值：阶码全 1
    • 阶码全 1、尾数全 0：无穷大
    • 阶码全 1、尾数不为 0：NaN，not a number

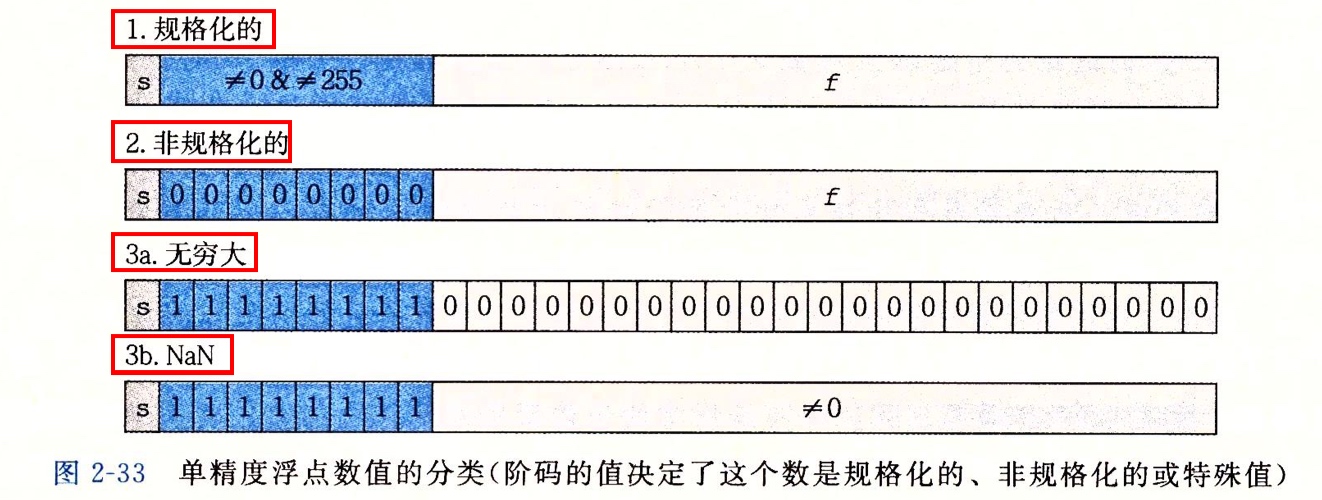
浮点数分类： 15751032439909

浮点数表示示例

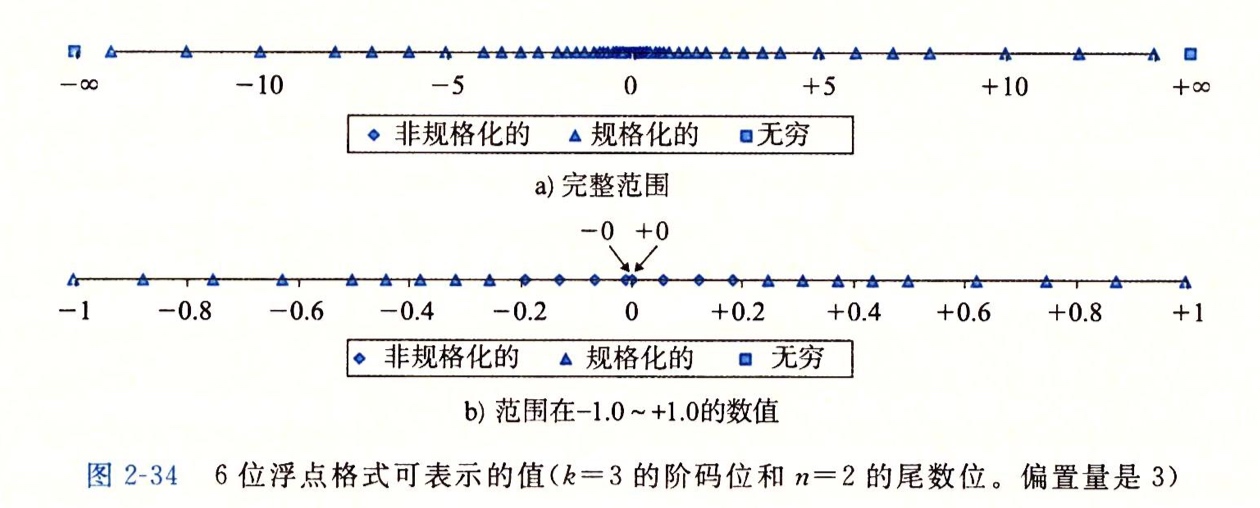
6 位 浮点数示例： 15751036989967

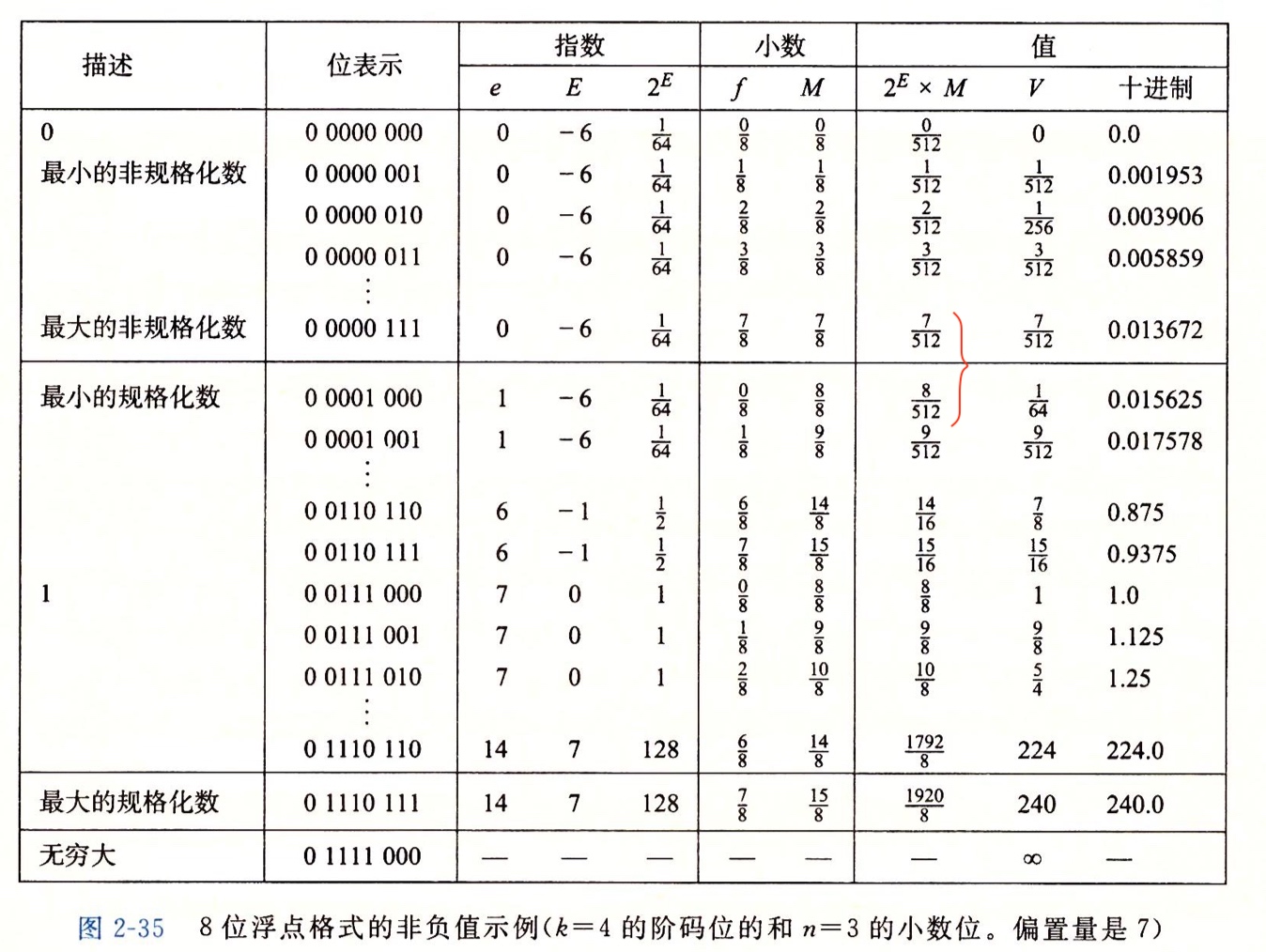
8 位浮点数的非负值示例，可以看到最大的非规格化数和最小的规格化数之间的平滑过渡： 15751038137166

浮点数比较大小

将浮点数的位级表示看作无符号数，直接比较。负数需要简单的额外处理。

浮点运算

浮点加法不具有结合性，因为可能溢出、丢失精度。

乘法同理，可以交换，不可以结合，也不具有分配性。但是乘法运算满足单调性，即只要 a、b、c≠NaN，那么如果 a≥b，就一定有 a*c≥b*c。

浮点数与整数的类型转换

int 是 32 位，float 的尾数位是 23 位，double 的尾数位是 52 位。

  • int → float：不会溢出，可能丢失精度
  • int/float → double：不会变
  • double → float：可能溢出，也可能丢失精度
  • float → double/int：值会向 0 舍入。这相当于把尾数位看作无符号数，丢弃掉多余的位

浮点数的舍入

浮点数相当于是一种近似表示。当某个数字的有效位数超过浮点数所能表示的最大精度时，需要舍入。

舍入共分为 3 种情况：进一、舍去、向偶数舍入。具体采用哪种舍入规则，是根据被舍掉的位与中间值的大小关系确定的。

中间值：先以十进制为例。比如 5.23500，保留两位小数。那么中间值就是 XX.YY50000…0，即第三位是 5，之后全是 0。

按照浮点数的舍入规则，5.23500 被舍掉的位等于中间值，需要向偶数舍入，得到 5.24；5.23510 被舍掉的位大于中间值，需要进一，得到 5.24；5.23410 被舍掉的位小于中间值，需要舍去，得到 5.23。

对于某个二进制小数，假设最后几位为 XYYY…，要舍入到 X 这一位：

  1. 如果 YYY… == 100…，即被舍掉的位等于中间值，需要向偶数舍入。向偶数舍入分为两种情况：
    • 如果 X 是 1，说明舍入后是奇数，要进一以得到到偶数
    • 如果 X 是 0，说明舍入后是偶数，直接舍去 YYY…
  2. 如果 YYY… > 100…，即大于中间值，要进一
  3. 如果 YYY… < 100…，即小于中间值，要舍去