📈【深入理解计算机系统】Labs：data-lab
实验环境
首先克隆项目，放在 ~/sandbox/CSAPP-Labs。也可以放在别的地方，不过注意修改下面 docker run 命令的挂载目录。
git clone https://github.com/imageslr/CSAPP-Labs.git
然后安装 docker，拉取镜像：
# 前提是安装了 docker
docker pull imageslr/csapp-env
最后启动容器，并将项目目录 ~/sandbox/CSAPP-Labs 挂载到容器内的 /csapp-labs 目录下：
docker run -it -v ~/sandbox/CSAPP-Labs/:/csapp-labs --privileged --name csapp-env imageslr/csapp-env /bin/bash
就可以在容器内编译、测试程序了。
其他说明见 datalab-handout/README。
附：
- 退出容器：
exit - 退出容器后重新进入容器：
docker start -i csapp-env - 如果容器内编译不成功，需要编辑
Makefile，删除CFLAGS中的-m32参数
测试程序
包含两个测试程序：dlc、btest：
dlc检查函数是否符合限制条件，包括操作符的种类、数量等。不符合规定，会输出 Warning；符合规定没有任何输出。dlc程序要求所有的变量声明都位于函数一开始，否则会报错parse error。btest使用多个测试用例检验函数的正确性。每次修改bits.c后，都需要重新执行make，以生成最新的btest程序。
以下是主要用法，详细文档见 datalab-handout/README：
# 检查函数是否符合限制条件
./dlc bits.c
./dlc -e bits.c # 输出每个函数使用的操作符数量
# 编译 btest
make
# 检验所有函数的正确性
./btest
./btest -h # 查看帮助信息与参数
./btest -f xxx # 只检验某个函数 xxx
./btest -f xxx -1 value1 -2 value2 # 只检验某个函数 xxx，并指定第 1、2 个参数的值
# 展示某个整数或浮点数的位级表示
./ishow 123123
./fshow 15213243
题目列表
- bitAnd：使用或、非实现与
- getByte：获取一个整数的某个字节
- logicalShift：实现逻辑右移
- bitCount：统计二进制中 1 的个数
- bang：不用
!计算!x - fitsBits：判断某个数字是否能由一个 n 位二进制数表示
- tmin：返回 2 的补码的最小值
- divpwr2：计算某个数除以 2 的倍数
- negate：返回 -x
- isPositive：判断一个数是否是整数
- isLessOrEqual：判断 x <= y
- ilog2：计算某个数 log2
- float_neg：浮点数取反
- float_i2f：整型数转为浮点数
- float_twice：浮点数乘 2
题解
完整代码：bits.c
1. bitAnd
使用或、非实现与：德摩根定律 / 对偶律。
2. getByte
获取一个整数的某个字节。注意 n 表示字节数，而右移是按位右移，一个字节等于 8 位，所以实际右移位数是 n << 3。
3. logicalShift
实现逻辑右移。思路很简单，只需要让 x 与后 (32-n) 位全为 1 的数作掩码运算。
难点：
- 在不允许使用减法的情况下，如何求一个数的负数？
- 在不允许直接声明超过 255（0xff）的整数的情况下，如何得到后 y 位全为 1 的数（如 0xfffff）？
- 当 n=0 时，0x1 左移 32 位会发生溢出，得到 0，这时该如何计算 $2^32$？
解决办法：
- 负数的计算方法：
-x = ~x + 1 - 要得到后 y 位全为 1 的数，可以用只有第 y+1 位为 1 的数减去 1：
1 << y - 1 - 可以利用 $2^n - 1 == 2*2^{n-1} - 1 = 2^{n-1}-1+2^{n-1}$ 来拆分 $2^n$，避免溢出
最终代码：
int logicalShift(int x, int n)
{
int pos = 32 + (~n + 1); // 1 向左移 32-n 位，再减 1，可以得到后 32-n 位全为 1 的二进制数
int y = 1 << (pos + ~1 + 1); // y == 2^{pos-1}
x = x >> n;
return x & (y + ~1 + 1 + y);
}
4. bitCount
我认为这道题是 data lab 里最难的题目。
如果允许使用循环的话，思路很简单：让 x 的每一位都移到最后一位，然后 x & 1 判断最后一位是否为 1。但是这里并不允许使用控制流。
参考这篇文章的代码：
int bitCount(int x) {
int _mask1 = (0x55)|(0x55<<8);
int _mask2 = (0x33)|(0x33<<8);
int _mask3 = (0x0f)|(0x0f<<8);
int mask1 = _mask1|(_mask1<<16);
int mask2 = _mask2|(_mask2<<16);
int mask3 = _mask3|(_mask3<<16);
int mask4 = (0xff)|(0xff<<16);
int mask5 = (0xff)|(0xff<<8);
int ans = (x & mask1) + ((x>>1) & mask1);
ans = (ans & mask2) + ((ans>>2) & mask2);
ans = (ans & mask3) + ((ans>>4) & mask3);
ans = (ans & mask4) + ((ans>>8) & mask4);
ans = (ans & mask5) + ((ans>>16) & mask5);
return ans;
}
主要采用了分治的思想。以某个 16 位数字为例，计算其中 1 的个数，可以这么算：
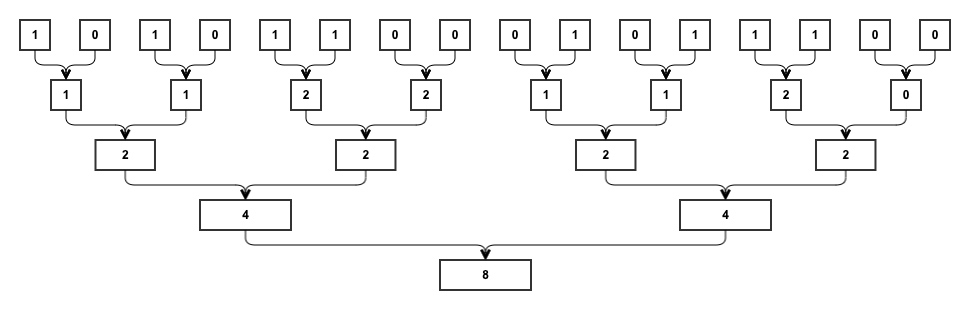即：先把每 1 位看成 1 组，两两相加，得到 8 组；然后再每 2 个组相加，得到 4 组…以此类推，直到得到 1 个数，这就是最终的结果。
上述过程用二进制可以这样表示：
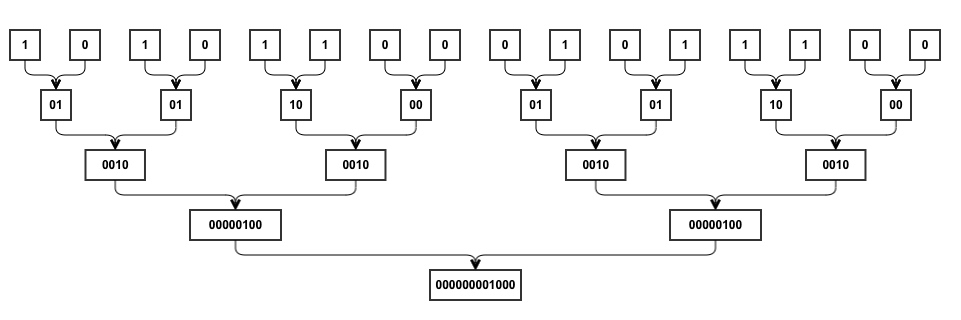
从上到下一共 5 行，每一行就是代码中 ans 经过一次计算后的二进制表示。因此我们只需要用代码实现这个分治过程即可。
先看怎么求一个 2 位二进制数 x 的 1 的个数：只需要计算 (x&1) + ((x>>1)&1)，x>>1表示将高 1 位移动到低 1 位。
这段代码有 5 个常数 mask1~mask5，分别为 0x55555555，0x33333333，0x0f0f0f0f，0x00ff00ff，0x0000ffff，二进制表示里分别间隔 1 个 0、2 个 0、4 个 0、8 个 0、16 个 0。
ans = (x&mask1) + ((x>>1)&mask1)就是上图第一行到第二行的过程ans = (ans & mask2) + ((ans>>2) & mask2)就是上图第二行到第三行的过程- …
ans 右移的位数和 mask 中连续的 0 的个数是一一对应的。以第二步为例，ans = (ans & mask2) + ((ans>>2) & mask2) 的过程可以形象化为：
ans: 01 01 10 00 01 01 10 00
两两相加：
[01 01] [10 00] [01 01] [10 00]
相当于：
00 01 00 00 00 01 00 00 // 这就是 ans & mask2
+ 00 01 00 10 00 01 00 10 // 这就是 (ans>>2) & mask2
= 0010 0010 0010 0010
最后，这里要注意运算符的优先级和结合性。测试发现 a & c + b 相当于 a & (c+b) 而不是 (a&c) + b，即 & 优先级比 + 高，但是按照 C 规范，加法的优先级应该比按位与高才对。
5. bang
不用 ! 计算 !x。
只有 0 和 -0 的最高位都不是 1，对于其他数字 x，x 或 -x 中总有一个最高位为1，因此只需要把 x 和 -x 或一下再判断高位就可以了。
6. fitsBits
判断某个数字是否能由一个 n 位二进制数表示。
将数字右移 n-1 位之后，应该要么是全 0，要么是全 1。全 1 的话，加个 1 就变成全 0 了。这道题允许用取反，因此可以这么写：
int fitsBits(int x, int n)
{
// ~1 +1 == ~0
return !(x >> (n + ~0)) | !((x >> (n + ~0)) + 1);
}
这两个判断可以合在一起：不管全 0 还是全 1，右移 n-1 位后加 1 再右移 1 位，都会变成全 0：
int fitsBits(int x, int n)
{
// ~1 +1 == ~0
return !(((x >> (n + ~0)) + 1) >> 1);
}
8. divpwr2
计算某个数除以 2 的倍数。对于正数来说，直接右移即可；对于负数来说，需要加一个 bias 以向 0 舍入。可以根据符号位是 0 还是 1 来决定要不要加 bias。
11. isLessOrEqual
判断 x <= y。这里的问题在于直接作减法可能会溢出。
需要分类讨论两个数字的符号，如果符号不同，只有 x 最高位是 1、y 最高位是 0 时才有 x <= y；如果符号相同，直接做减法也不会溢出。
int isLessOrEqual(int x, int y)
{
// y - x >= 0 直接做减法可能负溢出
int diffSign = !!((x >> 31) ^ (y >> 31));
int diff = y + ~x + 1;
// 符号不同，x 必然小于 0；符号相同，差非负，直接做减法不会溢出
return (diffSign & x >> 31) | (!diffSign & !(diff >> 31));
}
12. ilog2
计算某个数 log2，本质就是找到最左的 1 所在的位置。这道题也比较难。
可以采用二分法，不断缩小最高位 1 所在的区间，每次将区间缩小一半。
使用一个变量 ans 保存区间右下标，初始时为 0，即最低位：
- 先移动 16 位，然后判断是不是大于 0。如果大于 0，说明 1 所在位置是大于 16 的，
ans = ans + 16；如果是等于 0，那么说明 1 所在位置是小于 16 的。 - 下一次以 ans 为最低位，再右移 8 位，判断是否大于 0。如果大于 0，说明 1 所在位置在大于 8 位；如果等于 0，说明 1 所在位置是小于 8 的。
- …以此类推，相当于每一步都将 1 所在区间缩小一半，经过 5 次后，就确定了 1 的位置
int ilog2(int x)
{
// 要找左侧第一个 1 的位置
// 每次将区间大小缩小一半
// ans 为区间右边界。最低位为 0，ans 从 0 增加
int ans = 0;
ans = (!!(x >> 16)) << 4; // ans = ans + 16?
ans = ans + ((!!(x >> (8 + ans))) << 3); // ans = ans + 8?
ans = ans + ((!!(x >> (4 + ans))) << 2); // ans = ans + 4?
ans = ans + ((!!(x >> (2 + ans))) << 1); // ans = ans + 2?
ans = ans + (!!(x >> (1 + ans))); // ans = ans + 2?
return ans;
}
这道题和 4 题 bitCount 比较像，4 题是从小到大，每次将范围扩大一倍；而这道题是从大到小，每次将范围缩小一半。
最后要注意运算符优先级，x + y << 2 相当于 (x + y) << 2 而不是 x + (y << 2)。
13. float_neg
- 如何对某一位取反？
- 如何表示
111...1000..0？
unsigned float_neg(unsigned uf)
{
// 符号位取反
unsigned neg = uf ^ 0x80000000;
// 判断指数位 1~9 位是否全为 1，并且尾数位不为 0
unsigned nan = uf & 0x7fffffff;
if (nan > 0x7f800000) // 0x7f800000: 1~9位为 1
{
neg = uf;
}
return neg;
}
14. float_i2f
这道题同样很难，做了很久，主要考的是细节，另外运算符限制 30 个，需要对浮点数表示有深入理解。可以先不管运算符个数的限制，保证能通过 btest 的测试，再慢慢缩减运算符。
减少运算符个数的办法：
if (condition_a && condition_b)可以拆成两个 if，if 不算操作符，可以节省 1 个&&- 所有常量如
1<<31、(1<<23)-1，可以直接用十六进制表示出来
unsigned float_i2f(int x)
{
int pos = 31; // 左侧第一个 1 的位置，从左到右为 31~0
int signx = x & 0x80000000; // 符号位
int exp; // 指数位
int t, tt, shifted_bits, shifted_len, mask; // 临时变量
// 特殊情况，直接返回
if (x == 0)
{
return 0;
}
// 如果 x 为负数，将其取反
// 注意这里一定要取反，并且 x 取反后位级表示会发生改变，
// 第一个 1 的位置会改变，不仅仅只有符号位取反
if (signx)
{
x = -x;
}
// 找左侧第一个 1 的位置
// 能用 while，就不需要用 11 题的分治的方法了
while (!((1 << pos) & x))
{
pos -= 1;
}
// 尾数部分：把左侧第一个 1 移动到倒数第 24 位，需要根据 pos 对 x 左移或右移
if (pos < 23)
{
// 向左移位，不需要考虑舍入的问题
x <<= (23 - pos);
}
else
{
/**
* 向右移位，需要舍入
* 共分为 3 种情况：进一、舍去、向偶数舍入
* （这部分内容在书的第 86 页）
*
* 假设最后几位为 XYYY...，要舍入到 X 这一位：
*
* 1. 如果 YYY... == 100...，即等于中间值，需要向偶数舍入
* 向偶数舍入分为两种情况：
* 1.1 如果 X 是 1，说明舍入后是奇数，因此要进一
* 1.2 如果 X 是 0，说明舍入后是偶数，直接舍去 YYY...
*
* 其他情况就是向上或向下舍入：
* 2. 如果 YYY... > 100...，即大于中间值，要进一
* 3. 如果 YYY... < 100...，即小于中间值，要舍去
*
* 进一的时候可能溢出，因此要按照这个顺序：
* ① 先舍入
* ② 再判断是否溢出，如果溢出，pos + 1
* ③ 最后再移位 / 计算指数部分
*/
// 比较 YYY... 与 100...，YYY...是要被舍掉的位
shifted_len = pos - 23;
tt = 1 << shifted_len; // 00..1000..0
t = tt >> 1; // 00...100..0
mask = tt - 1; // 00...111..1
shifted_bits = x & mask;
// 向偶数舍入，且需要进 1
if (shifted_bits == t)
{
if (x & tt)
x += t;
}
// 向上舍入
if (shifted_bits > t)
{
x += t;
}
// 判断是否因为进一而溢出
if (x & (1 << (pos + 1)))
{
pos++;
}
// 移位
x = x >> shifted_len;
}
x &= 0x007fffff; // x 只保留尾数部分
// 指数部分：e = E + 2^7-1
exp = (pos + 127) << 23;
return x | signx | exp;
}
15. float_twice
运算规则：
- 0、无穷大、NaN 乘 2 后不变
- 规格化的数，乘 2 时指数 + 1
- 非规格化的数，尾数位溢出时指数才会 + 1，其他情况只需要尾数位左移 1 位。可以统一为指数位和尾数位整体左移 1 位
我的解答见源文件：bits.c
一个更精简的版本：
// https://zhuanlan.zhihu.com/p/38753345
unsigned float_twice(unsigned uf)
{
// 无穷和 NaN，乘 2 也是返回 uf 本身
if (((uf >> 23) & 0xff) == 0xff) { return uf; }
// 非规格化 == 阶码域全 0 ，所以保留符号位，再将 frac 左移一位即可，相当于乘 2 的一次幂
if (((uf >> 23) & 0xff) == 0x00) {
return (uf & (0x1 << 31)) | (uf << 1);
}
// 规格化，则将 uf 的指数位加 1
return uf + (1 << 23); // 这就相当于指数位 + 1
}
参考资料：
- 版权声明：本文采用知识共享 3.0 许可证 (保持署名-自由转载-非商用-非衍生)
- 发表于 2019-12-11