📝【LeetCode】124 二叉树中的最大路径和
这道题是 LeetCode 124 题。
给定一个非空二叉树,返回其最大路径和。注意,这里的“路径”并非自顶向下的单向路径,而是二叉树中任意连通的路径,可以在任一节点开始和结束。比如对于下图的二叉树,10->12->9 是一个最大路径:
-9
/ \
1 12
/ \
10 9
分析
首先定义“端点”的概念。一条路径有两个端点:起点和终点。比如上述示例中,10 为起点,9 为终点。
接下来分析问题。假设一棵二叉树根节点为 a,左右子树为 b、c:
a
/ \
b c
则包含根节点 a 的最大路径有以下 4 种情况:
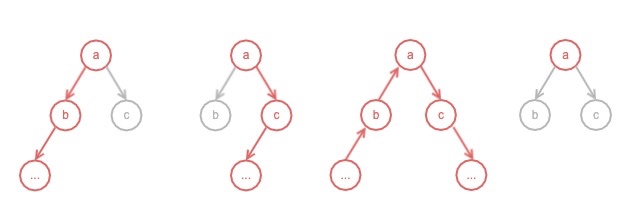
a+b->...,即节点 a+以 b 为起点的最大路径a+c->...,即节点 a+以 c 为起点的最大路径...->b->a+c->...,即以 b 为终点的最大路径+节点 a+以 c 为起点的最大路径- 只有
a,这种情况表示a没有子树,或者a的每个子树的最大路径和都是负数
因此,要想求包含根节点 a 的最大路径和,只需要知道 a 的左右子树中,以 a 的左右子节点 b、c 为端点的最大路径。显然,这是一个后序遍历的过程。
递归代码应该返回以根节点 a 为端点的最大路径和,即返回上述情况 1、2、4 的最大值,不含情况 3(a 为中间节点)。
整棵树的最大路径和应该在上述 4 种情况产生,这里使用一个全局变量。递归过程中,选择上述 4 种情况的最大值,更新全局变量。最后返回这个全局变量。
执行结果:
93/93 cases passed (16 ms)
Your runtime beats 97.26 % of golang submissions
Your memory usage beats 84.78 % of golang submissions (6.7 MB)
代码:
var res int
func maxPathSum(root *TreeNode) int {
res = -1 << 31 // 结果初始化为最小整数
dfs(root)
return res
}
func dfs(root *TreeNode) int {
if root == nil {
return 0
}
fromLeft := dfs(root.Left) // 以左子树为端点的最大路径和
fromRight := dfs(root.Right) // 以右子树为端点的最大路径和
fromRoot := Max( // 以 root 为端点的最大路径和,上图情况 1、2、4
root.Val,
Max(
root.Val+fromLeft,
root.Val+fromRight,
),
)
bypassRoot := root.Val + fromLeft + fromRight // 以 root 为中间节点的最大路径和,上图情况 3
res = Max(res, Max(bypassRoot, fromRoot))
return fromRoot // 返回以 root 为端点的最大路径和
}
func Max(a, b int) int {
if a > b {
return a
}
return b
}
进一步简化
如果某个节点的子树的最大路径和为负数,那么最大路径一定不包含这棵子树。这时不妨设该子树的路径和为 0,于是上述 4 种情况的路径和都可以合并为 1 种情况:root.Val + left + right。
代码十分简洁:
func dfs(root *TreeNode) int {
if root == nil {
return 0
}
left := Max(0, dfs(root.Left)) // 以左子树为端点的最大路径和
right := Max(0, dfs(root.Right)) // 以右子树为端点的最大路径和
res = Max(res, root.Val+left+right) // 包含 root 的
return Max(root.Val+left, root.Val+right) // 返回以 root 为端点的最大路径和
}
总结
本质上,这道题就是后序遍历。而难点在于,应该返回什么?
从上面的分析可知,递归代码返回的应该是以根节点为端点的最大路径和,而不是包含根节点的最大路径和。
在这种情况下,递归代码的返回值就不是最终结果了。我们需要使用一个全局变量,在递归过程中动态地更新其最大值。
本文发表在我的博客 https://imageslr.com/。我也会分享更多的题解,一起交流,共同进步!
- 版权声明:本文采用知识共享 3.0 许可证 (保持署名-自由转载-非商用-非衍生)
- 发表于 2020-02-25