📔【数据结构】各种排序算法
更多面试题总结请看:🗂【面试题】技术面试题汇总
综述
所有排序算法:
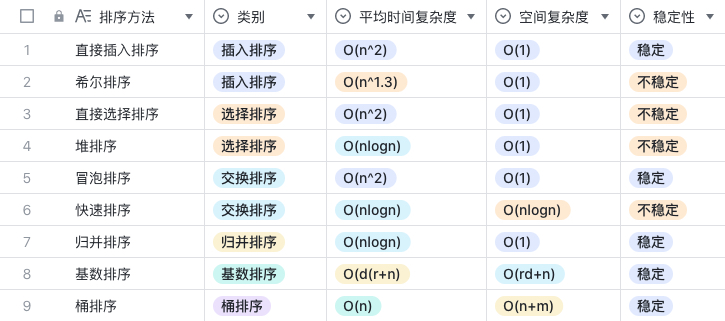
基数排序:r 代表关键字的基数,比如对十进制数字的 r==10;d 代表位数,比如
[0~999]范围内的数字的 d==3。
桶排序:m 代表桶的个数。
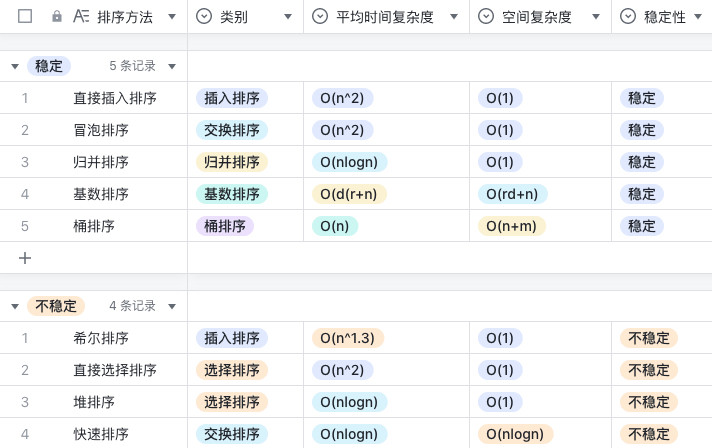
稳定的排序算法:冒泡排序、归并排序、基数排序、直接插入排序、桶排序。
不稳定的排序算法:快速排序、堆排序、直接选择排序、希尔排序。
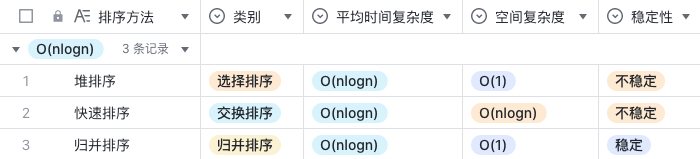
O(nlogn) 的排序算法:快速排序、堆排序、归并排序。
LeetCode 练习题
所有的排序算法都可以在 LeetCode 912. 排序数组 练习。模板:
class Solution {
public:
vector<int> sortArray(vector<int>& nums) {
xxxSort(nums); // TODO: 调用具体的排序算法
return nums;
}
void bubbleSort(vector<int>& nums) {}
void quickSort(vector<int>& nums) {}
// ...
};
冒泡排序
void bubbleSort(vector<int>& nums) {
int n = nums.size();
for (int i = 0; i < n-1; i++) { // i 表示已经排序的元素,排完 n-1 个后最后一个也不需要排了
for (int j = 1; j < n-i; j++) {
if (nums[j-1] > nums[j]) {
swap(nums[j-1], nums[j]);
}
}
}
}
插入排序
void insertSort(vector<int>& nums) {
int n = nums.size();
for (int i = 1; i < n; i++) {
int key = nums[i]; // 待排序元素
int j = i-1; // 已排序元素中最后一个不大于 key 的位置,key 将插在 j+1 的位置
while (j >= 0 && nums[j] > key) {
swap(nums[j], nums[j+1]);
j--;
}
nums[j+1] = key;
}
}
直接选择排序
void selectSort(vector<int>& nums) {
int n = nums.size();
for (int i = 0; i < n-1; i++) { // 最后一个不用排
int min = i;
for (int j = i+1; j < n; j++) {
if (nums[j] < nums[min]) {
min = j;
}
}
swap(nums[i], nums[min]);
}
}
快速排序
[0, last)表示所有小于pivot的元素集合,初始时last = 0表示区间为空- 选择左侧第一个元素作为
pivot - 不断地将小于
pivot的元素,移动到该区间里
void quickSort(vector<int> &nums) {
quickSort(nums, 0, nums.size() - 1);
}
void quickSort(vector<int>& nums, int start, int end) {
if (start >= end) return;
int pivot = partition(nums, start, end);
quickSort(nums, start, pivot-1);
quickSort(nums, pivot+1, end);
}
int partition(vector<int>& nums, int start, int end) {
int pivot = nums[start];
int last = start;
for (int i = start+1; i <= end; i++) {
if (nums[i] < pivot) {
swap(nums[i], nums[last++]);
swap(nums[last], nums[i]);
}
}
nums[last] = pivot;
return last;
}
归并排序
有递归法和迭代法两种实现方式。
递归法
void mergeSort (vector<int>& nums) {
mergeSort(nums, 0, nums.size() - 1);
}
void mergeSort(vector<int>& nums, int left, int right) {
if (left >= right) {
return;
}
int mid = (left + right) / 2;
mergeSort(nums, left, mid);
mergeSort(nums, mid + 1, right);
merge(nums, left, mid, right);
}
// 合并 [left, mid],[mid+1, right] 两部分有序数组
void merge(vector<int>& nums, int left, int mid, int right) {
vector<int> newNums(right - left + 1);
int c = 0, i = left, j = mid + 1;
while (i <= mid && j <= right) {
if (nums[i] < nums[j]) {
newNums[c] = nums[i];
c++;
i++;
} else {
newNums[c] = nums[j];
c++;
j++;
}
}
while (i <= mid) {
newNums[c] = nums[i];
c++;
i++;
}
while (j <= right) {
newNums[c] = nums[j];
c++;
j++;
}
for(i = left; i <= right; i++) {
nums[i] = newNums[i-left];
}
}
迭代法
void mergeSort(vector<int>& nums) {
int n = nums.size();
for (int s = 1; s < n; s*=2) { // 遍历所有可能的区间长度,注意这里的范围是 s < n,不能是 s <= n/2
for (int k = 0; k < n; k+=2*s) { // 找每个区间
int left = k,
mid = min(k+s, n),
right = min(k+2*s, n);
merge(nums, left, mid, right);
}
}
}
// 合并两个有序区间 [left, mid) 与 [mid, right),使 [left, right) 有序
// 注意区间是左闭右开,这是为了遵循 STL 的计算方式,可以简化代码(少很多 +1、-1)
void merge(vector<int>& nums, int left, int mid, int right) {
vector<int> arr(right-left);
int i = left, j = mid, k = 0;
while (i < mid && j < right) {
if (nums[i] < nums[j]) {
arr[k++] = nums[i++];
} else {
arr[k++] = nums[j++];
}
}
if (i < mid) copy(nums.begin()+i, nums.begin()+mid, arr.begin()+k);
if (j < right) copy(nums.begin()+j, nums.begin()+right, arr.begin()+k);
copy(arr.begin(), arr.end(), nums.begin()+left);
}
堆排序
- 分为“构建堆”、“堆排序”两个过程
- “构建堆”可以使用向上调整或向下调整,“堆排序”必须使用向下调整
- 升序 -> 构建最大堆,降序 -> 构建最小堆
向下调整建堆
void heapSort(vector<int>& nums) {
int n = nums.size();
// 构建堆
for (int i = n/2-1; i >= 0; i--) { // 从最后一个非叶节点开始,不断向下调整
heapAdjustDown(nums, i, n);
}
// 堆排序
for (int i = n-1; i > 0; i--) {
swap(nums[0], nums[i]); // 将堆顶元素弹出,和堆的末尾元素交换,此时 [i, n-1] 为排序后的区间,[0, i-1] 为堆的元素范围
heapAdjustDown(nums, 0, i); // 维护堆
}
}
// 向下调整,只调整下标为 s 的元素,堆的大小为 n
void heapAdjustDown(vector<int>& nums, int s, int n) {
int t = nums[s];
for (int i = 2*s+1; i < n; i = 2*i+1) {
if (i+1 < n && nums[i] < nums[i+1]) {
i++;
}
if (t >= nums[i]) { // 构建最大堆
break;
}
nums[s] = nums[i];
s = i;
}
nums[s] = t;
}
向上调整建堆
void heapSort(vector<int>& nums) {
int n = nums.size();
// 构建堆
for (int i = 0; i < n; i++) { // 从第一个节点开始遍历,直到最后一个节点,向上调整
headAdjustUp(nums, i);
}
// 堆排序
for (int i = n-1; i > 0; i--) {
swap(nums[0], nums[i]);
heapAdjustDown(nums, 0, i);
}
}
// 向上调整
void headAdjustUp(vector<int>& nums, int s) {
int t = nums[s];
// i 表示当前节点,手动计算父节点
for (int i = s; i > 0; i = (i - 1) / 2) {
if (nums[(i-1)/2] < t) {
nums[s] = nums[(i-1)/2];
s = (i - 1) / 2;
} else {
break;
}
}
nums[s] = t;
}
void heapAdjustDown(vector<int>& nums, int s, int n) {
int t = nums[s];
for (int i = 2*s+1; i < n; i = 2*i+1) {
if (i+1 < n && nums[i] < nums[i+1]) {
i++;
}
if (t >= nums[i]) {
break;
}
nums[s] = nums[i];
s = i;
}
nums[s] = t;
}
基数排序
- 一种非基于比较的排序算法
- 分别按照每一位进行排序,有最高位优先(Most Significant Digit first,MSD)和最低位优先(Least Significant Digit first,LSD)两种方法
- 基数排序以计数排序为基础,按照每一位排序时,实际上就是在进行计数排序
下面使用 LSD 方法实现基数排序。
举例
73, 22, 93, 43, 55, 14, 28, 65, 39, 81
对以上未排序数组,首先按照个位数的数值进行排序 —— 遍历每个数,并将其按照个位数分桶,对于同一个桶内的数字,维持其相对关系(稳定性):
[0] [1] [2] [3] [4] [5] [6] [7] [8] [9]
|-- --- --- --- --- --- --- --- --- --|
| 81 22 73 14 55 28 39|
| 93 65 |
| 43 |
随后依次串联桶中的数字,得到一个个位升序的序列:
81, 22, 73, 93, 43, 14, 55, 65, 28, 39
接着根据十位数分配:
[0] [1] [2] [3] [4] [5] [6] [7] [8] [9]
|-- --- --- --- --- --- --- --- --- --|
| 14 22 39 43 55 65 73 81 93|
| 28 |
随后依次串联桶中的数字,得到一个整体升序的序列:
14, 22, 28, 39, 43, 55, 65, 73, 81, 93
计数排序
计数排序的原理是:对于一个待排序序列中的某一个元素 x,一旦确定了该序列中小于 x 的元素的个数 c,就可以将 x 直接放在最终的有序序列的 c+1 位置上。计数排序的时间复杂度为 Ο(n+k),空间复杂度为 O(k),其中 n 为序列的元素个数,k 为元素的取值范围。代码如下:
#define K 1000000 // nums[i] 的取值范围,0~K
vector<int> aux(nums.size()); // 辅助数组,存放最终排序后的结果
vector<int> count(K, 0); // count[x] 表示值为 x 的元素的个数
for (int i = 0; i < nums.size(); i++) // 计数
count[nums[i]]++;
for (int i = 1; i < count.size(); i++) // 统计小于等于 nums[i] 的元素个数
count[i] += count[i - 1];
for (int i = nums.size() - 1; i >= 0; i--) // 从后往前遍历,将每个元素放到正确的位置
aux[--count[nums[i]]] = nums[i]; // TODO:先思考一下为什么这么写,再看下文的解释
for (int i = 0; i < nums.size(); i++) // 复制辅助数组
nums[i] = aux[i];
解释 aux[--count[nums[i]] = nums[i]:
count[nums[i]]表示小于等于nums[i]的元素个数,所以需要将nums[i]放到count[nums[i]] - 1的位置- 与
nums[i]相等的元素可能有多个,所以放完nums[i]以后需要将count[nums[i]]减 1,从而让后面的元素放到正确的位置 - for 循环是从后往前遍历,而值相等的元素也是从后往前放置到最终的数组中,因此保证了排序的稳定性
举例:给定待排序数组 [2(a), 2(b), 1, 3],有 count[1] == 1,count[2] == 3,count[3] == 4,各变量的变化过程如下:
当前元素 count[]数组 aux 数组
_ [0, 1, 3, 4] [_ _ _ _]
3 [0, 1, 3, 3] [_ _ _ 3]
1 [0, 0, 3, 3] [1 _ _ 3]
2(b) [0, 0, 2, 3] [1 _ 2(b) 3]
2(a) [0, 0, 1, 3] [1 2(a) 2(b) 3]
基数排序
vector<int> radixSort (vector<int>& nums) {
int maxVal = *max_element(nums.begin(), nums.end());
int exp = 1; // 1, 10, 100, 1000 ...
int radix = 10; // 基数为 10
vector<int> aux(nums.size()); // 存放最终结果
/* LSD Radix Sort */
while (maxVal / exp > 0) { // 从低位向高位,遍历每一位
// 这里是计数排序的代码
vector<int> count(radix, 0);
for (int i = 0; i < nums.size(); i++)
count[(nums[i] / exp) % 10]++; // 统计当前位为 0~9 的元素数量
for (int i = 1; i < count.size(); i++)
count[i] += count[i - 1];
for (int i = nums.size() - 1; i >= 0; i--)
aux[--count[(nums[i] / exp) % 10]] = nums[i];
for (int i = 0; i < nums.size(); i++)
nums[i] = aux[i];
exp *= 10;
}
return aux;
}
值得注意的是,上面的代码仅适用于所有元素都是非负数的情况。如果元素中存在负数,则需要将所有元素都加一个 offset 使其变为非负数,再进行基数排序。排序后,再将所有元素都减掉 offset。
vector<int> sortArray(vector<int>& nums) {
int minVal = *min_element(nums.begin(), nums.end());
int offset = minVal < 0 ? -minVal : 0;
for (int i = 0; i < nums.size(); i++) nums[i] += offset;
nums = radixSort(nums);
for (int i = 0; i < nums.size(); i++) nums[i] -= offset;
return nums;
}
桶排序
[TODO]
希尔排序
略。
不同排序算法的适用场景
- 若 n 较小(如 n≤50),可采用直接插入或直接选择排序。
- 若文件初始状态基本有序,则应选用直接插人、冒泡或随机的快速排序。
- 若 n 较大,则应采用时间复杂度为 O(nlogn) 的排序方法:快速排序、堆排序或归并排序。
- 当待排序的关键字是随机分布时,快速排序的平均时间最短。
- 堆排序所需的辅助空间少于快速排序,并且不会出现快速排序可能出现的最坏情况。
- 若要求排序稳定,则可选用归并排序。
- 归并排序需要较大的额外空间,但归并排序可以多路归并。
- 相比于从长度为 1 的序列开始归并,归并排序也可以和直接插入排序结合使用,先通过直接插入排序获得较长的有序序列,然后再进行归并。这种方式依然是稳定的。
大部分情况可以直接使用快速排序。
当待排序的关键字无法全部加载到内存中时,需要使用归并排序进行外部排序。
- 版权声明:本文采用知识共享 3.0 许可证 (保持署名-自由转载-非商用-非衍生)
- 发表于 2021-05-12,更新于 2021-05-12