📝【LeetCode】42 接雨水
这道题是 LeetCode 42 题。
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
这道题乍一看和 LeetCode 84 柱状图中最大的矩形很像。事实上,84 题的很多解法都可以套到这道题上。
通用的优化方法
这道题有一个通用的优化方法。把柱子想象成下图的曲线,雨水只能存储在柱子之间的“谷”里,因此可以跳过左侧和右侧的上升坡,只遍历中间的柱子。
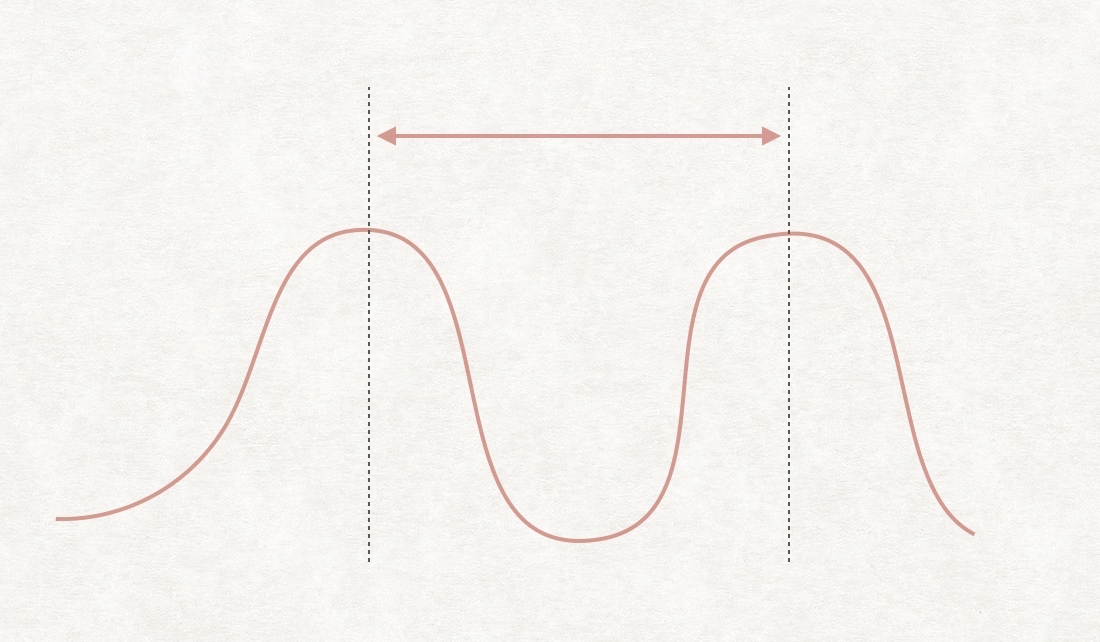
定义两个变量 left、right 分别表示上图两个虚线,始终令 left 右侧递减,right 左侧递增,只需要遍历区间 [left,right]。这是一种“双指针”的思想。
这种情况下,left、right 是一个「峰值」,即它们比自己左右的柱子都高。当 left >= right 时,说明所有柱子中已经不存在“谷”了,可以结束了。
left, right := trimLeftRight(heights)
if left >= right {
return res
}
func trimLeftRight(heights []int) (int, int) {
n := len(heights)
left, right := 0, n-1
for left < right && heights[left] <= heights[left+1] {
heights[left] = 0
left++
}
for right > left && heights[right] <= heights[right-1] {
heights[right] = 0
right--
}
return left, right
}
解法一:暴力(遍历不同的高度)
这种解法对应于 84 题的解法一, 84 题的解法一是使用一根从下到上、逐渐升高的水平线,统计水平线下方的连续矩形面积。这道题也可以使用类似的思路。
如下图所示,先统计所有高度为 1 的雨水的体积,然后所有柱子高度都减 1,继续重复此过程,直到所有柱子高度为 0。
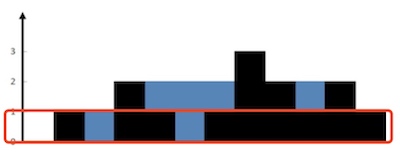
在每一轮统计之前,需要使用上文所说的优化方法,跳过区间左右侧的斜坡。这样可以保证:每遇到一个高度为 0 的柱子,它的上方一定可以接雨水,左右一定有比它高的柱子。因此只要遇到一个高度为 0 的柱子,雨水总量就增加 1 单位。
时间复杂度:O(m×n),m 为柱子的最大高度,n 为柱子个数。
空间复杂度:O(1)。
执行结果:960 ms
315/315 cases passed (960 ms)
Your runtime beats 5.14 % of golang submissions
Your memory usage beats 100 % of golang submissions (2.8 MB)
代码:
func trap(heights []int) int {
if len(heights) == 0 {
return 0
}
n := len(heights)
m := 0
for _, h := range heights {
m = Max(m, h)
}
res := 0
left, right := 0, n-1
for ; m > 0; m-- {
left, right = trimLeftRight(heights)
if left >= right {
return res
}
for i := left; i <= right; i++ {
if heights[i] == 0 {
res++
} else {
heights[i]--
}
}
}
return res
}
解法二:暴力(遍历不同的柱子)
这种解法对应于 84 题的解法四,思路是一列一列地求每一列上方能接多少雨水。
对于每一个柱子,只需要向左、向右找到最高的柱子,如果左右最高的柱子都比它高,那么这个柱子上方一定可以接到雨水。能接多少雨水,取决于左右最高的柱子的较小值。设柱子 i 左右最高的柱子下标分别为 left、right,则柱子 i 可以接雨水:
Min(height[left], height[right]) - height[i]
相当于依次计算下图红色区域的面积:
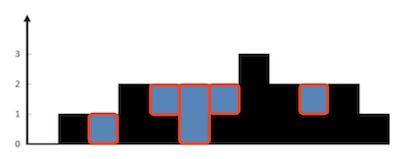
时间复杂度:O(n2)。
空间复杂度:O(1)。
执行结果:80 ms
315/315 cases passed (80 ms)
Your runtime beats 11.68 % of golang submissions
Your memory usage beats 75.85 % of golang submissions (2.8 MB)
代码:
func trap(heights []int) int {
if len(heights) == 0 {
return 0
}
left, right := trimLeftRight(heights)
if left >= right {
return 0
}
res := 0
for i := left + 1; i <= right-1; i++ { // 左右边界上一定没雨水
hLeft, hRight := 0, 0
for j := left; j < i; j++ {
hLeft = Max(hLeft, heights[j])
}
for j := i + 1; j <= right; j++ {
hRight = Max(hRight, heights[j])
}
h := heights[i]
if hLeft > h && hRight > h {
res += Min(hLeft, hRight) - h
}
}
return res
}
解法三:使用线段树优化解法二
解法二需要查询区间最值,可以使用线段树来优化,从而将查询区间最值的时间由 O(n) 降为 O(logn)。84 题的解法三也采用了这种思路。
关于线段树的实现,可以查看我之前的文章。本题线段树仅需要构建和查询,不需要更新,实现并无难度,都是很简单的递归。引入线段树后,解法二只需要更改两行代码。
时间复杂度:O(nlogn)。
空间复杂度:O(n),线段树的空间开销。
执行结果:时间大幅缩短,仅需 8ms
315/315 cases passed (8 ms)
Your runtime beats 22.64 % of golang submissions
Your memory usage beats 5.1 % of golang submissions (4.3 MB)
代码:
func trap(heights []int) int {
if len(heights) == 0 {
return 0
}
left, right := trimLeftRight(heights)
if left >= right {
return 0
}
res := 0
sTree := BuildSegmentTree(heights, 0, len(heights)-1) // 1. 构建线段树
for i := left + 1; i <= right-1; i++ { // 左右边界上一定没雨水
hLeft := sTree.Query(left, i-1) // 2. 使用 Query() 方法查找区间最值
hRight := sTree.Query(i+1, right)
h := heights[i]
if hLeft > h && hRight > h {
res += Min(hLeft, hRight) - h
}
}
return res
}
type SegmentTreeNode struct {
start int
end int
max int
left *SegmentTreeNode
right *SegmentTreeNode
}
func BuildSegmentTree(nums []int, left, right int) *SegmentTreeNode {
if left > right {
return nil
}
root := &SegmentTreeNode{left, right, nums[left], nil, nil} // 根据节点区间的左边界值初始化
if left == right {
return root
}
mid := (left + right) / 2
root.left = BuildSegmentTree(nums, left, mid)
root.right = BuildSegmentTree(nums, mid+1, right)
root.max = Max(root.left.max, root.right.max)
return root
}
func (root *SegmentTreeNode) Query(start, end int) int {
if start <= root.start && end >= root.end {
return root.max
}
if start > root.end || end < root.start {
return math.MinInt32
}
return Max(root.left.Query(start, end), root.right.Query(start, end))
}
func Min(a, b int) int {
if a > b {
return b
}
return a
}
func Max(a, b int) int {
if a > b {
return a
}
return b
}
解法四:使用动态规划优化解法二
优化部分还是如何求左右区间最值。
对于解法二,求每个元素左右的最值时,都会涉及很多重复计算。比如求 i=3 左侧的最大值,需要遍历前 3 个元素,找出最大值;而在求 i=4 左侧的最大值时,又需要遍历前 4 个元素,找出最大值。但此时我们发现,前 3 个元素之前已经找过最大值了,只需比较 前 3 个元素的最大值 和 第 4 个元素 哪个大就可以了。
这是一种动态规划的思路,设 maxLeft[i]、maxRight[i] 分别表示下标 i 的柱子左右区间的最大值,则状态转移方程为:
maxLeft[i] = Max(maxLeft[i-1], heights[i-1])
maxRight[i] = Max(maxRight[i+1], heights[i+1])
时间复杂度:O(n)。
空间复杂度:O(n)。
执行结果:0ms,不愧是 O(n) 的解法,比线段树更优
315/315 cases passed (0 ms)
Your runtime beats 100 % of golang submissions
Your memory usage beats 14.63 % of golang submissions (3.1 MB)
代码:
func trap(heights []int) int {
if len(heights) == 0 {
return 0
}
left, right := trimLeftRight(heights)
if left >= right {
return 0
}
n := len(heights)
res := 0
maxLeft, maxRight := make([]int, n), make([]int, n)
maxLeft[0], maxRight[n-1] = 0, 0
for i := 1; i < n; i++ {
maxLeft[i] = Max(maxLeft[i-1], heights[i-1])
}
for i := n - 2; i >= 0; i-- {
maxRight[i] = Max(maxRight[i+1], heights[i+1])
}
for i := left + 1; i <= right-1; i++ { // 左右边界上一定没雨水
hLeft, hRight := maxLeft[i], maxRight[i]
h := heights[i]
if hLeft > h && hRight > h {
res += Min(hLeft, hRight) - h
}
}
return res
}
解法五:使用双指针优化解法四
解法四的空间复杂度为 O(n),但是每个 maxLeft[i] 都只被使用了一次,按道理可以优化为 O(1)。
回顾二维 dp 数组优化为一维 dp 数组的过程:如果一个位置的状态依赖于其左、上两个位置的值,那么只需采用“行从上到下、列从左到右”的顺序遍历每个位置。反之,如果依赖的是右、上的值,那需要采用“行从上到下、列从右到左”的顺序遍历每个位置。
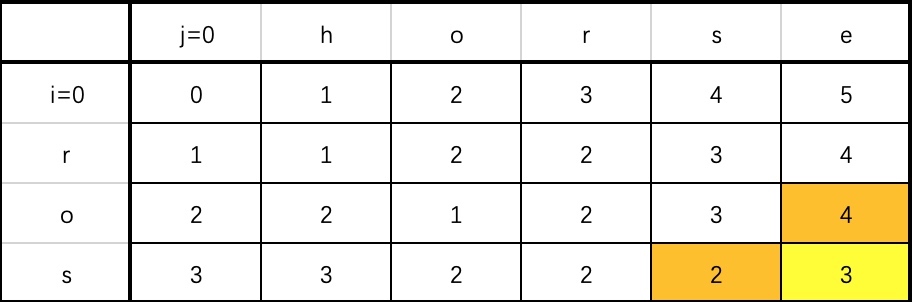
分析我们为什么采用这种顺序。在二维数组里,更新每个位置 dp[i][j] 时,需要知道 dp[i-1][j] 和 dp[i][j-1]。而压缩为一维数组后,一维数组的每个位置 dp[j] 在更新前就相当于二维数组的 dp[i-1][j],在更新后相当于 dp[i][j]。
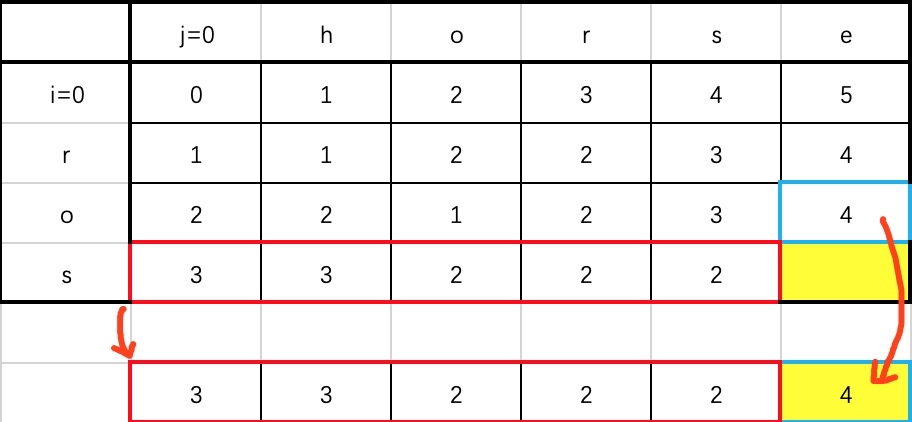
在这道题中,我们有两个一维 dp 数组,maxLeft[] 从左到右更新,maxRight[] 从右到左更新,如下图所示:
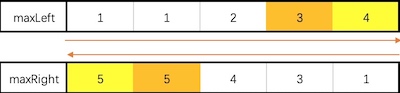
如果从左到右遍历,那只能将 maxLeft[] 压缩为一个变量:
maxRight := make([]int, n) // maxRight 还是一个一维数组
maxRight[n-1] = heights[n-1]
for i := n-2; i >= 0; i-- { // 需要提前从右往左遍历,求出每个 maxRight[i]
maxRight[i] = Max(maxRight[i+1], heights[i+1])
}
maxLeft := heights[0] // maxLeft 压缩为一个变量
for i := 1; i < n; i++ {
maxLeft = Max(maxLeft, heights[i-1])
// ...
}
反之,如果从右到左遍历,那只能将 maxRight[] 压缩为一个变量。
如果我们希望同时将 maxLeft[]、maxRight[] 压缩为两个变量 maxLeft、maxRight,那应该采用何种顺序遍历?答案是同时从左右两个方向遍历。
引入两个指针 left 和 right,从两个方向遍历。定义 maxLeft 表示柱子 left 左侧的最大高度,maxRight 表示柱子 right 右侧的最大高度。
计算每个柱子能接多少雨水,只需要知道左右两侧最高柱子的最小值。因此,如果 maxLeft <= maxRight,那么可以肯定柱子 left 右侧的最大高度一定 大于等于 maxRight,因此柱子 left 左右两侧最高柱子的最小值一定是 maxLeft。
同理,如果 maxLeft >= maxRight,那么可以肯定柱子 right 左侧的最大高度一定 大于等于 maxLeft,因此柱子 right 左右两侧最高柱子的最小值一定是 maxRight。
这样,我们就可以根据 maxLeft 与 maxRight 的大小关系,选择是从左到右遍历,还是从右到左遍历。如果 maxLeft <= maxRight,则 left 右移,同时更新 maxLeft;否则,right 左移,同时更新 maxRight。
时间复杂度:O(n)。
空间复杂度:O(1)。
执行结果:同解法四。
代码:
func trap(heights []int) int {
if len(heights) == 0 {
return 0
}
left, right := trimLeftRight(heights)
if left >= right {
return 0
}
res := 0
left, right = left+1, right-1 // 左右边界一定无法接雨水
maxLeft, maxRight := heights[left-1], heights[right+1] // 初始化
for left <= right {
if maxLeft <= maxRight { // 从左向右
h := heights[left]
if maxLeft > h {
res += maxLeft - h
}
maxLeft = Max(maxLeft, h)
left++
} else { // 从右向左
h := heights[right]
if maxRight > h {
res += maxRight - h
}
maxRight = Max(maxRight, h)
right--
}
}
return res
}
解法六:单调栈
这种解法对应于 84 题解法五。在 84 题的解法五中,我们使用单调栈找到某个柱子左右第一个比它矮的柱子。而在这道题中,我们可以使用单调栈找到某个柱子左右第一个比它高的柱子。思路和 84 题解法五一模一样!只是单调栈由递增变为了递减。
如果我们能依次求出下图红色区域的面积,那么就能得到雨水的总量:
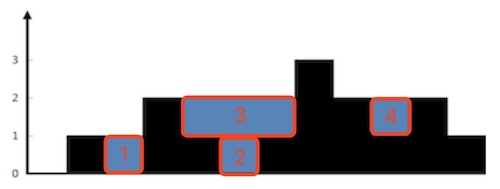
下面推导如何计算其中每一个红色区域的面积。
设单调栈保存柱子的下标,从左到右遍历每个柱子。如果当前柱子 i 的高度大于栈顶元素的高度,则栈顶元素 stack[top] 右侧第一个比它高的柱子的下标就是 i,左侧第一个比它高的柱子的下标就是 stack[top-1]。
令 left = stack[top-1],right = i,top = stack[top],如下图所示,可以计算出 left、right、top 三根柱子包围的雨水量为:
(Min(heights[left], heights[right]) - heights[top]) × (right-left-1)
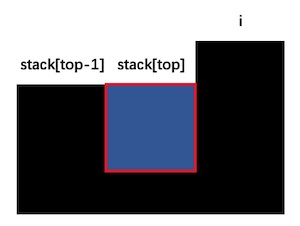
算法流程可以表述为:
- 从左到右遍历所有元素
- 如果当前元素的高度小于等于栈顶元素的高度,就将当前下标入栈
- 否则,不断将栈顶元素出栈,同时根据上述公式计算雨水量
- 重复第 3 步,直到当前元素的高度不大于栈顶元素的高度,然后将当前下标入栈
注意:第 3 步弹出栈顶元素后,必须判断栈是否为空。只有弹出一个元素后栈不为空,才能保证弹出元素左侧有比它更高的元素,这时才能接到雨水。
时间复杂度:O(n)。 空间复杂度:O(n)。
执行结果:同解法四。
代码:
func trap(heights []int) int {
if len(heights) == 0 {
return 0
}
left, right := trimLeftRight(heights)
if left >= right {
return 0
}
res := 0
stack := NewStack()
for i := left; i <= right; i++ { // 从 1 开始遍历
for !stack.Empty() && heights[i] > heights[stack.Top()] {
h := heights[stack.Pop()] // 弹出栈顶元素
if stack.Empty() { // 弹出元素后栈不能为空
break
}
left, right := stack.Top(), i
res += (Min(heights[left], heights[right]) - h) * (right - left - 1)
}
stack.Push(i)
}
return res
}
// 以下是栈的模板代码
type ElementType = int
type Stack struct {
s []ElementType
}
func NewStack() *Stack {
return &Stack{
s: make([]ElementType, 0),
}
}
func (s *Stack) Empty() bool {
return len(s.s) == 0
}
func (s *Stack) Top() ElementType {
if s.Empty() {
return 0
}
return s.s[len(s.s)-1]
}
func (s *Stack) Pop() ElementType {
if s.Empty() {
return 0
}
t := s.s[len(s.s)-1]
s.s = s.s[:len(s.s)-1]
return t
}
func (s *Stack) Push(v ElementType) {
s.s = append(s.s, v)
}
总结
本文提供了 6 种解法,解法二到解法六都可以看作同一种思路。可以看到,即使是相同的思路,采用不同的方法实现,也会有不同的时间效率。
本题涉及线段树、动态规划、单调栈的应用,值得细细品味。同时,本题的大部分解法都和 84 题的解法 一一对应,同一种解法在不同的题目间举一反三,更能加深理解。大家也可以去看看 84 题。
本文发表在我的博客 https://imageslr.com。我也会分享更多的题解,一起交流,共同进步!
- 版权声明:本文采用知识共享 3.0 许可证 (保持署名-自由转载-非商用-非衍生)
- 发表于 2020-02-21